| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- 동적프로그래밍
- google coding competition
- AI
- 그래프
- 리눅스
- CSS
- 프로그래밍
- 코딩테스트
- linux
- 운영체제
- 코딩
- 백준
- nlp
- OS
- dp
- 브루트포스
- BFS
- 순열
- kick start
- 킥스타트
- 딥러닝
- 프로그래머스
- 동적 프로그래밍
- DFS
- PYTHON
- 네트워크
- 알고리즘
- 파이썬
- 코딩 테스트
- 구글 킥스타트
- Today
- Total
오뚝이개발자
[CH2] 퍼셉트론(Perceptron) 본문
퍼셉트론(Perceptron)이란?
다수의 신호를 입력으로 받아 하나의 신호를 출력하는 알고리즘으로 신경망(딥러닝)의 기원이다.
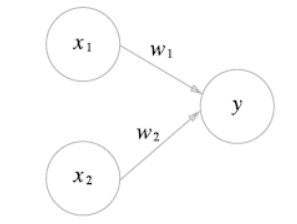
위의 그림에서 원을 '노드(뉴런)'이라고, w1과 w2를 가중치라고 부른다. 위의 퍼셉트론을 수식으로 나타내면 다음과 같다.
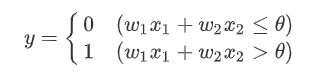
즉, w1x2 + w2x2의 값이 세타보다 작거나 같으면 0을, 크면 1을 출력한다. 이 때, 세타를 임계값이라 한다. 다시말하면, 신호의 총합이 임계값을 넘을 때만 1을 출력하는데 이를 "뉴런이 활성화"되었다고 한다. 가중치는 각 신호가 결과에 주는 영향력을 조절하는 역할을 한다.
기계학습이란?
기계학습에서 '학습'이란 위와 같은 퍼셉트론의 적절한 매개변수 값을 컴퓨터가 자동으로 정하게 하는 것을 말한다. 그렇다면 사람이 하는 일은 무엇일까? 바로 구조(모델)을 고안하고, 컴퓨터에 적절한 학습데이터를 주는 것이다.
AND 게이트 퍼셉트론으로 구현
논리회로에서 기본 단위가 되는 단순한 논리 gate들엔 and, or, nand, xor이 있다. 이 중 and 게이트를 퍼셉트론으로 구현해보자. and 게이트의 진리표는 아래와 같다.

import numpy as np
# AND gate 구현
def AND(x1, x2):
w1, w2, theta = 0.5, 0.5, 0.7
tmp = x1*w1 + x2*w2
if tmp <= theta:
return 0
elif tmp > theta:
return 1
print(AND(0,0), AND(1,0), AND(0,1), AND(1,1)) # 0 0 0 1
가중치와 편향을 도입한 AND 게이트 구현
위의 퍼셉트론 수식에서 세타를 -b로 치환하면 아래와 같은 수식이 된다.
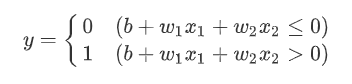
이 때, b를 편향(bias)라고 한다. 편향은 뉴런이 "얼마나 쉽게 활성화"되는지를 조절한다. 이를 도입하여 AND, NAND, OR 게이트를 구현해보자. 각 게이트는 가중치와 편향의 값만 달라진다.
import numpy as np
# 가중치, 편향 도입한 AND gate 구현
def AND(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(AND(0,0), AND(1,0), AND(0,1), AND(1,1)) # 0 0 0 1
# NAND gate 구현
def NAND(x1, x2):
x = np.array([x1, x2])
w = np.array([-0.5, -0.5])
b = 0.7
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(NAND(0,0), NAND(1,0), NAND(0,1), NAND(1,1)) # 1 1 1 0
# OR gate 구현
def OR(x1, x2):
x = np.array([x1, x2])
w = np.array([0.5, 0.5])
b = -0.2
tmp = np.sum(w*x) + b
if tmp <= 0:
return 0
else:
return 1
print(OR(0,0), OR(1,0), OR(0,1), OR(1,1)) # 0 1 1 1
퍼셉트론의 동작 시각화
퍼셉트론의 동작을 시각화하여 알아보자. OR을 예로 들어보자. (b, w1, w2) = (-0.5, 1.0, 1.0)일 때 수식은 아래와 같다.

이를 그래프로 나타내면 다음과 같다.

OR게이트는 (x1, x2) = (0,0) 일 때 0, (x1, x2) = (1,0), (0,1), (1,1)일 때 1이다. 그래프를 보면 직선이 이 두 영역을 분할하는 것을 알 수 있다. 즉, 단층 퍼셉트론은 이처럼 "직선"으로 나뉜 두 영역을 만든다.
XOR 게이트의 동작 시각화
이러한 퍼셉트론도 한계가 있는데 바로 XOR 게이트를 구현하지 못한다는 것이다. XOR 게이트의 진리표는 아래와 같다.

이를 OR게이트에서 한 것처럼 그래프로 나타내면 다음과 같이 된다.
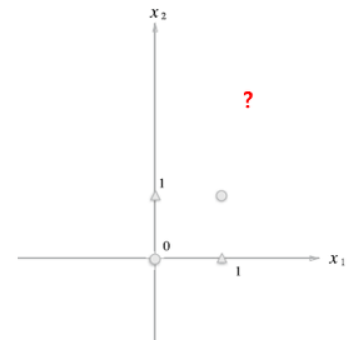
XOR 게이트의 그래프를 OR 게이트와 같이 "직선"으로 분할할 수 있을까? 답은 '불가능하다'이다. XOR 게이트의 그래프를 분할하기 위해서는 아래와 같은 "곡선"이어야 한다.

정리하자면, 단층 퍼셉트론은 직선 하나로 나눈 영역만 표현이 가능하다는 한계가 있다는 것이다. 즉, 비선형 영역을 분리해내지 못한다는 것이다.
이러한 한계점을 어떻게 극복할 수 있을까?
이러한 고민에서 나온 것이 바로 층을 쌓아 깊게 만드는 다층 퍼셉트론(multi-layer perceptron)이다. XOR 게이트는 AND, NAND, OR 게이트를 조합해서 만들 수 있다.
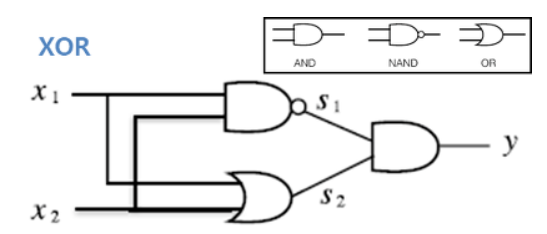
이를 진리표로 나타내면 아래와 같다.

이러한 XOR 게이트의 동작을 퍼셉트론으로 시각화하면 아래와 같다.

코드로 구현하면 아래와 같다.
# XOR gate 구현
def XOR(x1, x2):
s1 = NAND(x1, x2)
s2 = OR(x1, x2)
y = AND(s1, s2)
return y
print(XOR(0,0), XOR(1,0), XOR(0,1), XOR(1,1)) # 0 1 1 0결론을 내자면, 다층 퍼셉트론은 단층으로 구현하지 못한 것을 층을 쌓아 깊게 만들어 구현할 수 있다. 이처럼 퍼셉트론은 층을 깊게 쌓아 더 다양한 것을 표현하는 것이 가능하다.
NAND에서 컴퓨터까지
사실 퍼셉트론으로 '컴퓨터'마저도 구현이 가능하다. 근본적으로 컴퓨터의 원리 또한 퍼셉트론처럼 결국 입력과 출력으로 구성된 특정 규칙대로 계산을 수행하는 것이기 때문이다. 실제로 The Elements of Computing System: Building a Modern Computer from First Principles(The MIT Press, 2005)라는 책은 "NANA에서 테트리스까지!"라는 구호 아래 만들어졌다고 한다. NAND라는 단순한 소자만으로 복잡한 컴퓨터라는 시스템을 만들어 낼 수 있다는 사실이 놀랍다.
'AI > 밑바닥딥러닝1' 카테고리의 다른 글
| [CH6] 학습 관련 기술들 (0) | 2020.06.21 |
|---|---|
| [CH5] 오차역전파법 (0) | 2020.06.20 |
| [CH4] 신경망 학습 (0) | 2020.06.19 |
| [CH3] 신경망 (0) | 2020.06.13 |
| [CH1] Numpy, Matplotlib 실습 (0) | 2020.06.09 |




