| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 그래프
- PYTHON
- OS
- 코딩 테스트
- 순열
- AI
- kick start
- 구글 킥스타트
- linux
- DFS
- 코딩
- 네트워크
- 동적 프로그래밍
- 딥러닝
- google coding competition
- nlp
- 프로그래머스
- 프로그래밍
- dp
- 운영체제
- CSS
- 백준
- 동적프로그래밍
- 브루트포스
- 코딩테스트
- 파이썬
- 알고리즘
- 킥스타트
- BFS
- 리눅스
- Today
- Total
오뚝이개발자
선형회귀(linear regression), 라쏘(LASSO), 리지(Ridge) 본문
선형 회귀는 사용되는 특성(feature)의 갯수에 따라 다음과 같이 구분된다.
- 단순 선형 회귀(simple linear regression) : 특징이 1개
- 다중 선형 회귀(multiple linear regression) : 특징이 여러개
LASSO와 Ridge는 선형 회귀의 단점을 보완해 범용성을 부여하기 위해 만들어진 도구들이다.
선형 회귀란?
예컨대, 어묵을 팔고 있는 사람이 기온에 따른 자신의 어묵 판매량을 알아보기 위해 상관관계를 조사했다고 하자. 그 결과 기온이 낮은 날에는 어묵 판매량이 늘어나는 경향이 있었다. 이를 바탕으로 경향성을 분석하자 y=ax+b와 같은 선형 관계가 나타났다. 덕분에 어묵 장수는 자신의 다음 날의 기온을 일차함수식에 넣어 판매량을 예측한 뒤 필요한 만큼의 재료를 준비하여 신선한 상태로 어묵을 판매할 수 있었고, 입소문이 나 손님들로 북적거리게 되었다.
단순 선형 회귀
단순 선형 회귀란 단 하나의 특징(feature)을 가지고 라벨값(label) 혹은 타깃(target)을 예측하기 위한 회귀 모델을 찾는 것이다.

파란색 점은 여러 샘플(sample)이고 x축은 샘플의 특징값, y축은 라벨값을 나타낸다. 위 그래프에선 특징값이 커지면 라벨값도 커지는 경향을 보이고 있다. 이 현상을 가장 잘 설명해주는 선형함수를 찾아낸 것이 빨간색 선이다. 이처럼 선형함수가 주어지면 새로운 데이터의 특징값이 주어졌을 때 라벨값을 예측할 수 있다. 단순 선형 회귀를 위한 식을 일반화해 나타내면 아래와 같다.
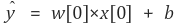
좌변의 y^는 예측값, x가 특징이다. 1차 함수의 관점에서 보자면 w는 기울기 b는 y절편이지만 여기서는 w를 가중치, b를 편향이라고 보는 것이 더 적절하다. 여러 샘플들을 이용해 가장 최적의 w와 b를 찾아야 하는데 보통 경사하강법을 사용한다.
다중 선형 회귀
위의 오뎅 예시에선 단 하나의 특징, 기온을 가지고 회귀 모델을 만들었다. 하지만 특징 하나만을 가지고는 정확한 예측이 어렵다. 요일에 따라 판매량이 달라질 수 있고, 비나 눈이 오는지에 따라서도 달라질 수 있다. 이처럼 하나가 아닌 여러 개의 특징을 활용해 회귀 모델을 만드는 것을 다중 선형 회귀라 한다. 다중 선형 회귀의 예측 함수는 아래와 같다.
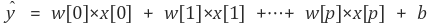
여기서 특성은 총 p+1개, 그에 따라 가중치도 p+1개이다. 주어진 여러 샘플들의 p+1개의 특징(x[0]~x[p])과 라벨값(y) 사이의 관계를 잘 나타내주는 w와 b를 찾아야 한다. 특징이 1개인 선형 회귀에선 모델이 직선이었지만, 2개면 평면이 되고, 그 이상이면 초평면(hyperplane)이 된다.
최적의 가중치와 편향 찾기
선형 회귀에서 어떻게 최적의 가중치와 편향을 찾아낼 수 있을까? 이 부분이 중요하다. 바로 라벨값(y)과 예측값(y^) 사이의 평균제곱오차(Mean Squared Error, MSE)를 최소화하는 파라미터 w와 b를 찾으면 된다.


그런데 다중 선형 회귀 모델은 과적합(overfitting)되는 경향이 있다. 필요이상으로 자세하게 특징값과 라벨값의 관계를 분석했다는 것이다. 이로 인해 일반화 능력(범용능력)이 떨어져 새로운 데이터를 제대로 예측하지 못한다. 이를 해결하기 위한 것이 바로 라쏘(LASSO)와 릿지(Ridge)이다.
라쏘(LASSO)
기존의 선형 회귀에선 적절한 가중치와 편향을 찾아내는 것이 관건이었다. 라쏘는 거기에 추가적인 제약 조건을 준다. 바로 MSE가 최소가 되게 하는 가중치와 편향을 찾으면서 동시에, 가중치들의 절댓값의 합이 최소가 되게 한다는 것이다. 다시 말해, 가중치의 모든 원소가 0이 되거나 0에 가깝게 되도록 해야 한다. 따라서 어떠한 특징들은 모델을 만들 때 사용되지 않기도 한다. 어떤 벡터 요소의 절댓값의 합은 L1-norm이다. 즉, 라쏘는 L1-norm 페널티를 가진 선형 회귀 방법이다. 식은 아래와 같다.

m은 가중치의 갯수(혹은 특징의 갯수)이고, α는 페널티의 효과를 조절해주는 하이퍼파라미터다. 이 값이 커지면 페널티 항의 영향력이 커지고, 작아져서 거의 0이 되면 선형 회귀와 같아진다. MSE와 penalty항의 합이 최소가 되게 하는 w와 b를 찾는 것이 바로 라쏘의 목적이다.

그런데 이러한 방법이 어떻게 범용성을 부여해 과적합을 방지하는 것일까? 우선 MSE항이 작아질수록 라벨값과 예측값들의 차이가 작아지고, L1-norm이 작아질수록 많은 가중치들이 0이 되거나 0에 가까워진다는 것을 기억하자. α가 크면 전체값(MSE+penalty)이 L1-norm의 영향을 크게 받아 L1-norm을 작게 만드는 것이 우선시된다. 반면, α가 작으면 MSE가 작아지게 하는 것에 더 비중을 두게 된다. 따라서, α가 너무 작으면 overfitting(복잡도가 너무 큼)이, 너무 크면 underfitting(복잡도가 너무 작음)이 일어난다. α는 하이퍼파라미터로 cross-validation을 통해 적절한 값을 설정해주어야한다.
라쏘의 장점은 크게 두가지다.
- 첫번째는 제약 조건을 통해 일반화된 모형을 찾는다는 것이다.
- 두번째는 가중치들이 0이 되게 함으로써 그에 해당하는 특성들을 제외해준다. 결과적으로 모델에서 가장 중요한 특성이 무엇인지 알게되는 등 모델 해석력이 좋아진다.
릿지(Ridge)
마지막으로 라쏘와 굉장히 유사한 릿지에 대해 간단히만 언급하자면 패널티 항에 L1-norm 대신에 L2-norm 패널티를 가진다. 차이가 있다면 라쏘는 가중치들이 0이 되지만, 릿지의 가중치들은 0에 가까워질 뿐 0이 되지는 않는다. 특성이 많은데 그중 일부분만 중요하다면 라쏘가, 특성의 중요도가 전체적으로 비슷하다면 릿지가 좀 더 괜찮은 모델을 찾아줄 것이다.
출처
'AI > 밑바닥딥러닝1' 카테고리의 다른 글
| [핸즈온ML] CH3. 분류 (0) | 2020.07.17 |
|---|---|
| [핸즈온ML] CH1. 한눈에 보는 머신러닝 (0) | 2020.07.13 |
| Bias와 Variance (0) | 2020.07.06 |
| L1, L2 regularization (0) | 2020.06.28 |
| 오버피팅(overfitting) 방지법 정리 (0) | 2020.06.27 |




