| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 프로그래밍
- 코딩테스트
- linux
- 코딩 테스트
- 알고리즘
- dp
- 프로그래머스
- 킥스타트
- nlp
- 파이썬
- DFS
- 순열
- 동적프로그래밍
- 딥러닝
- OS
- PYTHON
- 구글 킥스타트
- 동적 프로그래밍
- 코딩
- 그래프
- 백준
- 네트워크
- kick start
- 리눅스
- 브루트포스
- AI
- CSS
- BFS
- 운영체제
- google coding competition
- Today
- Total
오뚝이개발자
[자료구조 및 알고리즘] CH12. Dynamic programming(동적프로그래밍) 본문
Dynamic programming이란?
-
일반적으로, 분할정복 알고리즘과 유사하게 큰 문제를 더 작은 문제로 나누어 푸는 기법(역시 최적해를 찾는데 사용되는 경우가 많다.)
-
결정적인 차이점은 다음과 같다.
-
동적 프로그래밍의 경우 작은 문제들이 반복된다.(피보나치의 경우 f(5)를 구하기 위해선 f(4),f(3)이 필요한데 f(4)를 구하기 위해 f(3)이 다시 필요하다.)
-
동적 프로그래밍의 경우 작은 문제들의 답이 항상 같다는 것이다.
-
-
따라서, 위의 경우처럼 반복되는 계산을 줄이기 위해 메모이제이션(Memoization)을 사용
-
실제로 피보나치 수열을 구하는 함수를 구현할 때, 재귀로 구현하게 되면 반복되는 계산으로 인해 수가 커지면 실행시간이 아주 오래 걸리지만, 동적 프로그래밍으로 구현하면 금방 해결된다.
-
메모이제이션을 위해 recurrence equation을 찾는 것이 중요!!!
-
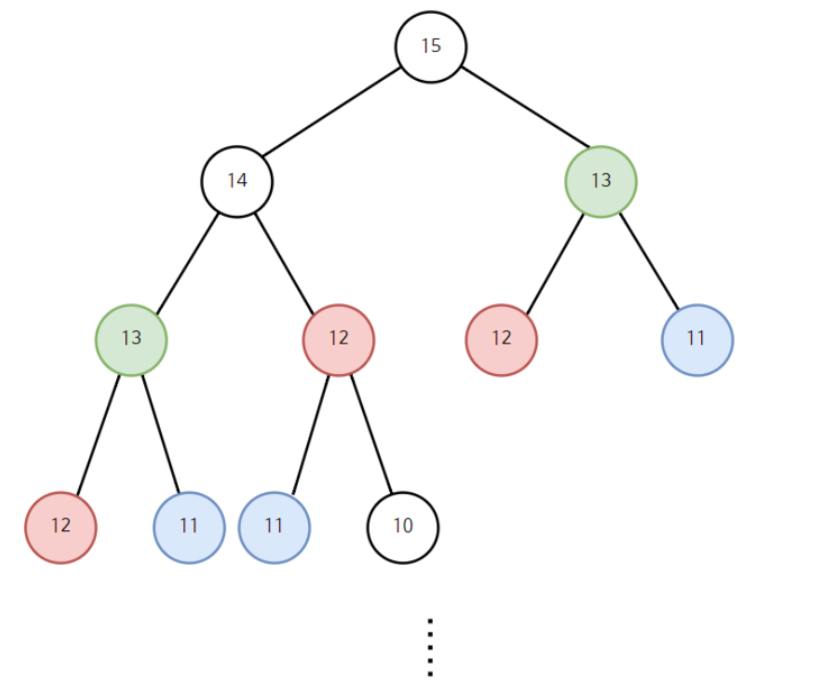
Dynamic algorithm을 구현하는 두 가지 방법
-
Top-down
-
가장 큰 문제를 먼저 방문해 작은 문제들을 호출해가며 답을 찾는 방법
-
// top-down
int fibonacci(int n)
{
if (n == 0) return 0;
if (n == 1) return 1;
if (dp[n] != -1) return dp[n];
dp[n] = fibonacci(n - 1) + fibonacci(n - 2);
return dp[n];
}
-
Bottom-up
-
가장 작은 문제들부터 답을 찾아가서 큰 문제에 도달하는 방법
-
// bottom-up
int fibonacci(int n)
{
dp[0] = 0, dp[1] = 1;
for (int i = 2; i <= n; i++)
dp[i] = dp[i - 1] + dp[i - 2];
}
Floyd's shortest path algorithm
-
이전에 탐용법을 이용한 다익스트라 알고리즘으로 최소비용거리를 구해보았는데 동적프로그래밍을 활용하는 플로이드 알고리즘으로도 구현할 수 있다.
-
c(i,j,k)가 i에서 j로 가는데 중간에 k보다 큰 index를 갖는 vertex가 없는 최소비용거리라고 하자. 그럼 아래와 같이 구현할 수 있다.
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
c(i,j,k)=min{c(i,j,k-1), c(i,k,k-1)+c(k,j,k-1)}'CS 기초 > 자료구조 및 알고리즘' 카테고리의 다른 글
| [자료구조 및 알고리즘] 너비우선탐색(BFS) (0) | 2020.10.27 |
|---|---|
| [자료구조 및 알고리즘] 깊이우선탐색(DFS) (0) | 2020.10.27 |
| [자료구조 및 알고리즘] CH11. Greedy algorithm (0) | 2020.10.27 |
| [자료구조 및 알고리즘] CH10. Divide and Conquer (0) | 2020.10.27 |
| [자료구조 및 알고리즘] CH9. Sorting and Searching (0) | 2020.10.26 |



